调了一下午,我人都傻了。
二叉查找树的定义:
左儿子值小于当前节点值,右儿子值大于当前节点值。
查找性能与树深同阶,这意味着树深维持在$O(log(n))$附近时查找性能最优秀。
但是根节点选取不恰当会导致树深接近$O(n)$,退化成一条链。
给出一棵树:
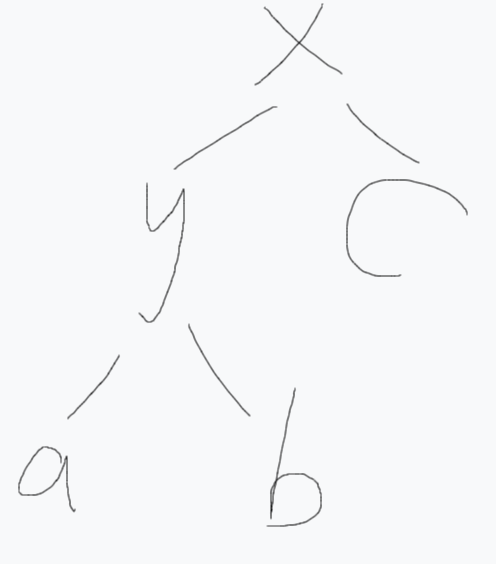
树示意图1
其中$x$、$y$为两个节点,$a$、$b$、$c$为子树。
经过左旋后可以得到:
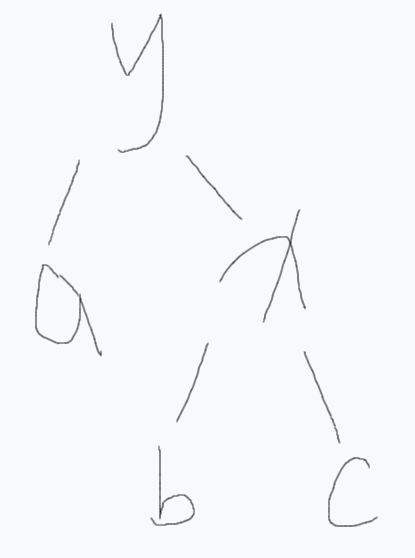
树示意图2
很容易看出自旋之后没有改变二叉查找树的性质。
一句话总结:
左旋操作就是令$x_{left}=y_{right}$,令$y_{right}=x$。
代码如下:
void spin(int &p,int d) {// d为旋转方向
int k=s[p][d];
s[p][d]=s[k][!d];
s[p][!d]=p;
up(p);
up(k);
p=k;
}
事实上$treap$是$tree$和$heap$的结合,它在保证自己满足二叉查找树的性质的同时,为每个节点附加了一个随机值$key$,而且使得$key$满足小顶堆的性质。
每个节点保存如下信息:
- 储存的值$val$
- 优先级$key$
- 左右儿子指针$ls$、$rs$
- 必要时还需要存储某节点所在子树大小$sz$和节点数字个数$num$
这样的好处是相同的数字存储到了相同的节点当中去,减少节点数量。
此外,手写的inline随机函数可以对运行时间有常数上的优化。
下面是封装后的结构体,支持查询前缀和后缀的编号,每一次查询一定要记得清空答案:
struct treap {
int seed;
inline int rand(){ seed=seed*49147LL%INT_MAX; return seed; }
int l[maxn],r[maxn],val[maxn],key[maxn],sz[maxn],w[maxn];
int tot,rt,ans;
treap(){ seed=233; }
inline void up(int p){ sz[p]=sz[l[p]]+sz[r[p]]+w[p]; }
void lspin(int &k) {
int t=r[k];
r[k]=l[t];
l[t]=k;
sz[t]=sz[k];
up(k);
k=t;
}
void rspin(int &k) {
int t=l[k];
l[k]=r[t];
r[t]=k;
sz[t]=sz[k];
up(k);
k=t;
}
void ins(int &k,int x){
if(!k) {
++tot;
k=tot;
sz[k]=w[k]=1;
val[k]=x;
key[k]=rand();
return;
}
sz[k]++;
if(val[k]==x) w[k]++;
else if(val[k]<x){
ins(r[k],x);
if(key[r[k]]<key[k]) lspin(k);
//maintain a small heap
}
else {
ins(l[k],x);
if(key[l[k]]<key[k]) rspin(k);
//maintain a small heap
}
}
void del(int &k,int x) {
if(!k) return;
//can't find x
if(val[k]==x) {
if(w[k]>1) {
w[k]--;
sz[k]--;
return;
}
if(l[k]==0||r[k]==0)
k=l[k]+r[k];
else if(key[l[k]]<key[r[k]]) {
rspin(k);
del(k,x);
}
else {
lspin(k);
del(k,x);
}
}
else if(val[k]<x) {
sz[k]--;
del(r[k],x);
}
else {
sz[k]--;
del(l[k],x);
}
}
int ask(int k,int x) {
if(!k) return 0;
if(val[k]==x) return sz[l[k]]+1;
else if(x>val[k]) return sz[l[k]]+w[k]+ask(r[k],x);
else return ask(l[k],x);
}
int get(int k,int x) {
if(!k) return 0;
if(x<=sz[l[k]]) return get(l[k],x);
else if(x>sz[l[k]]+w[k]) return get(r[k],x-sz[l[k]]-w[k]);
else return val[k];
}
void pre(int k,int x) {
if(!k) return;
if(val[k]<x) ans=k,pre(r[k],x);
else pre(l[k],x);
}
void suc(int k,int x){
if(!k) return;
if(val[k]>x) ans=k,suc(l[k],x);
else suc(r[k],x);
}
};