考虑对一棵树维护以下操作:
- $xy$路径上所有节点权值$+z$
- 求$xy$路径上所有节点权值和
- 以$x$为根的子树内所有节点权值$+z$
- 求$x$为根的子树内节点权值和
树链剖分的想法是是把树拆分成链,再用线段树维护链上的性质。
拆分链的方法是关键,最好使得链的数量保持在logn左右。
定义:
重儿子为当前节点的包含子节点数最多的那个子节点。
如下图:
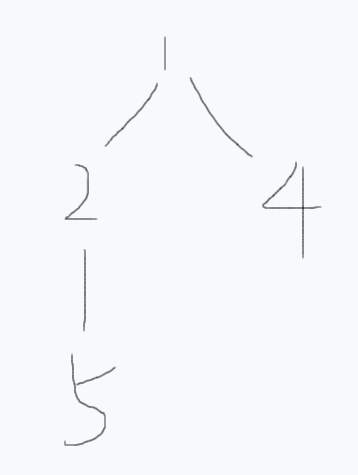
树示意图1
其中2是1的重儿子。
那么如何求解重儿子?你需要先准备一大堆数组:
int head[maxn],to[maxn],e[maxn];//Graph
int sz[maxn],fa[maxn],dep[maxn],son[maxn];//using for d1
int top[maxn],ord[maxn],rord[maxn],last[maxn];//using for d2
int tg,td,tt;//three timers,using for label graph,dfs and segment tree
struct segment_tree{
int l,r,v,ls,rs,tag;
};//segment tree
之后一遍dfs即可,此外还需要预处理一些其他的信息:
void d1(int x) {
sz[x]=1;
for(int i=head[x];i;i=to[i]){
int y=e[i];
if(y==fa[x]) continue;
fa[y]=x;//change y's father
dep[y]=dep[x]+1;//the depth of x
d1(y);
sz[x]+=sz[y];//change x's size
if(sz[y]>sz[son[x]])
son[x]=y;//change the heavy son
}
}
定义:
重链是由重儿子所组成的链。
注意重链可能并不互相连接,并且单个点也有可能构成重链。
如下图:
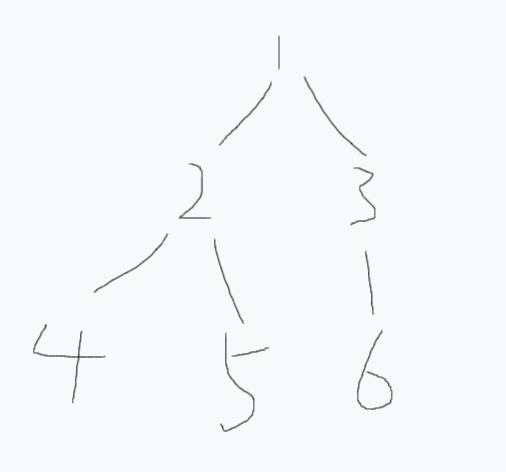
树示意图2
图中共三条重链:分别是$1\rightarrow2\rightarrow4$、$5$以及$3\rightarrow6$。
树链剖分遵循一种特别的dfs序,处理时一直沿着重链向下,之后处理其他链。
原因有二:
- 对某个节点,其重链直到叶节点都连续
- 重链条数维持在$log(n)$附近
void d2(int x,int t) {
top[x]=t;//the point on the top of heacy chain
ord[x]=++td;//the dfs order
rord[td]=x;//which point dfs order refers to
if(son[x]) d2(son[x],t);
for(int i=head[x];i;i=to[i]) {
int y=e[i];
if(y!=fa[x]&&y!=son[x])
d2(y,y);
}
last[x]=td;//modify the points under x
}
然后建立线段树,注意线段树是建立在$dfs$序上的,时刻注意$ord$和$rord$的关系:
ord把原来的节点映射到dfs序,rord把dfs序映射回原来的节点。
void build(int x,int y) {
++tt;
tr[tt].l=x;
tr[tt].r=y;
tr[tt].tag=0;
if(x==y) {
tr[tt].ls=tr[tt].rs=0;
tr[tt].v=w[rord[x]];
return;
}
else {
int tmp=tt,m=x+y>>1;
tr[tmp].ls=tt+1,build(x,m);
tr[tmp].rs=tt+1,build(m+1,y);
up(tmp);
}
}
可以看出这种建立线段树的方式类似于动态开点,所以需要保存左右子节点的指针。
考虑如何使用这种结构维护$xy$的$lca$:
- 让$xy$所在重链的顶端深度更大的向上跳,直到它们位于同一条重链。
- 每一次上跳需要跳到当前重链的$top$处,再跳向父节点。
- 每次$modify$当前节点到重链顶端节点的一段区间,最后维护$x$到$y$的区间。
考虑这样一种情况:
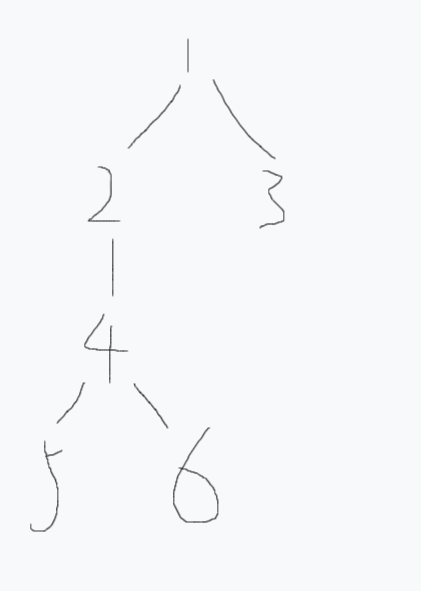
树示意图3
假设$x$为$5$,$y$为$3$:
- 如果谁深度更大谁跳向重链顶端,$x$会直接跳到$1$,然后再也找不到父亲,陷入死循环。
- 但是如果比较$x$和$y$所在重链的顶端,会发现$3$的重链顶端深度更大,因为$3$所在的重链就是他本身。
- 现在$3$上跳,就能顺利找到$lca$。
代码如下:
void modify_xy(int x,int y,int z) {
while(top[x]!=top[y]) {
if(dep[top[x]]>dep[top[y]])
swap(x,y);
modify(1,ord[top[y]],ord[y],z);
//the dfs order of the top point is smaller than the points under it
y=fa[top[y]];
}
if(dep[x]>dep[y]) swap(x,y);
modify(1,ord[x],ord[y],z);
}
int sum_xy(int x,int y) {
int ans=0;
while(top[x]!=top[y]) {
if(dep[top[x]]>dep[top[y]])
swap(x,y);
ans+=sum(1,ord[top[y]],ord[y]);
ans%=P;
y=fa[top[y]];
}
if(dep[x]>dep[y]) swap(x,y);
ans+=sum(1,ord[x],ord[y]);
ans%=P;
return ans;
}
最后考虑如何搞子树。
有这样一个结论:
实际上一棵子树当中所有节点的编号一定是连续的
所以last[x]是x所在子树的最后一个叶节点的dfs序
每次维护子树只需要维护[ord[x],last[x]]这段区间即可
问题迎刃而解。
代码如下:
void modify_x(int x,int z) {
modify(1,ord[x],last[x],z);
}
int sum_x(int x) {
int ans=sum(1,ord[x],last[x]);
ans%=P;
return ans;
}
/*
modify和sum函数按照普通打区间修改标记的线段树写法去搞就好
*/
void up(int p) {
tr[p].v=tr[tr[p].ls].v+tr[tr[p].rs].v;
}
void down(int p) {
if(tr[p].tag!=0){
tr[tr[p].ls].v+=tr[p].tag*(tr[tr[p].ls].r-tr[tr[p].ls].l+1);
tr[tr[p].rs].v+=tr[p].tag*(tr[tr[p].rs].r-tr[tr[p].rs].l+1);
tr[tr[p].ls].tag+=tr[p].tag;
tr[tr[p].rs].tag+=tr[p].tag;
tr[p].tag=0;
}
}
int sum(int p,int x,int y) {
if(x<=tr[p].l&&tr[p].r<=y) return tr[p].v;
int ans=0,m=tr[p].l+tr[p].r>>1;
down(p);
if(x<=m) ans+=sum(tr[p].ls,x,y);
ans%=P;
if(y>m) ans+=sum(tr[p].rs,x,y);
ans%=P;
up(p);
return ans;
}
void modify(int p,int x,int y,int z) {
if(x<=tr[p].l&&tr[p].r<=y) {
tr[p].v+=z*(tr[p].r-tr[p].l+1);
tr[p].tag+=z;
return;
}
int m=tr[p].l+tr[p].r>>1;
down(p);
if(x<=m) modify(tr[p].ls,x,y,z);
if(y>m) modify(tr[p].rs,x,y,z);
up(p);
}