一种“可持久化”的线段树,可以记录某个历史版本对应的值。
假设现在有一棵树如下图这样:
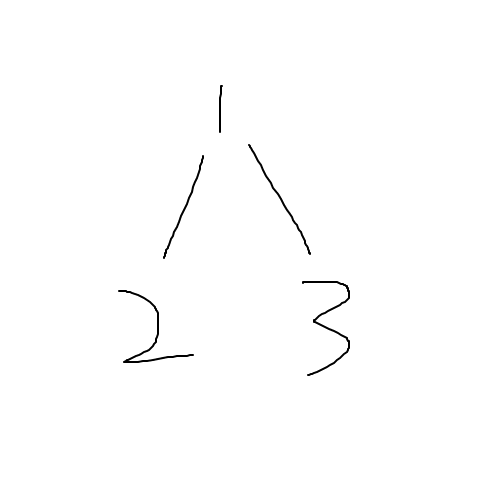
第一步
假设现在要修改$3$节点对应的区间,那么先复制出一个根$1’$,再复制一个修改过的$3’$,连接成下图这样:
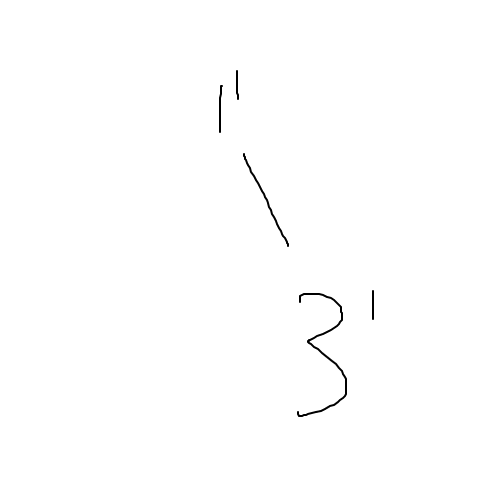
第二步
最后一步,把那些没修改的节点跟新建的根连接起来像下图这样:
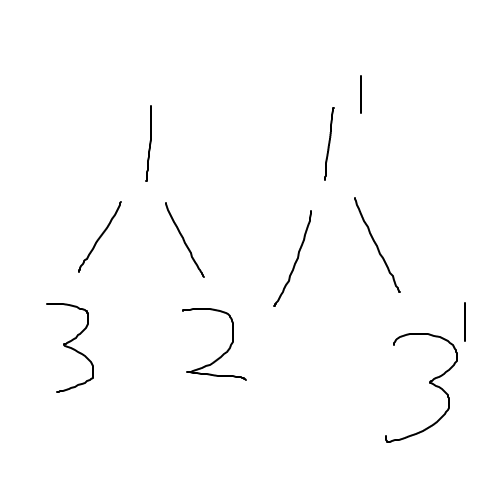
第三步
这样只需要记录某个历史版本对应的根就可以访问这个版本的全部值了,每次修改时间复杂度$O(log(n))$。
为了查询静态区间第$k$大,需要在值域上建立主席树,每次插入一个数就新开一个历史版本。
如果需要查询$[L,R]$区间的第k大,只需要考虑$[L-1,R]$区间中哪些数字被加了一即可,类似于前缀和。
静态区间第$k$大的模板如下:
int n,m,l,r,k;
int a[maxn],tmp[maxn],org[maxn],tot=0;
int rt[maxn];// 储存根的编号
struct node {
// 主席树结构体,ll和rr分别代表左右儿子,cnt记录区间和,每次更改必须要传入参数l和r,代表该节点表示的区间
int ll,rr,cnt;
}tr[maxn*300];
int build(int l,int r) {// 建立空主席树,动态开点,返回根节点编号
int p=++tot;
tr[p].cnt=0;
if(l==r) return p;
int m=l+r>>1;
tr[p].ll=build(l,m);
tr[p].rr=build(m+1,r);// 连接左右儿子
return p;
}
int change(int rt,int l,int r,int x,int y) {// 更改区间的值
int p=++tot;
tr[p]=tr[rt];
if(l==r){
tr[p].cnt++;
return p;
}
int m=l+r>>1;
if(y<=m) tr[p].ll=change(tr[rt].ll,l,m,x,y);
else tr[p].rr=change(tr[rt].rr,m+1,r,x,y);
// 因为每次更新只涉及到一个点,所以只向着一边重建,跟x没什么关系,这样写是为了区间修改的操作
tr[p].cnt=tr[tr[p].ll].cnt+tr[tr[p].rr].cnt;// 向上更新
return p;
}
int ask(int p,int q,int l,int r,int k) {// 询问函数
int sum=tr[tr[q].ll].cnt-tr[tr[p].ll].cnt;
int m=l+r>>1;
if(l==r) return l;// 得到答案
if(sum>=k) return ask(tr[p].ll,tr[q].ll,l,m,k);// 左区间数字个数多于k
else return ask(tr[p].rr,tr[q].rr,m+1,r,k-sum);// 左区间数字个数少于k
}
int main() {// 主函数
scanf("%d%d",&n,&m);
rt[0]=build(1,n);// 获得第一版根
for(int i=1;i<=n;++i) {
scanf("%d",&a[i]);
tmp[i]=a[i];
}
sort(tmp+1,tmp+1+n);
for(int i=1;i<=n;++i) {
int k=lower_bound(tmp+1,tmp+1+n,a[i])-tmp;
org[k]=a[i],a[i]=k;
}
// 离散化
for(int i=1;i<=n;++i)
rt[i]=change(rt[i-1],1,n,1,a[i]);// 在上一版根的基础上插入新值,注意那个1,a[i]只是做做样子,真正起作用的是a[i]
for(int i=1;i<=m;++i) {
scanf("%d%d%d",&l,&r,&k);
printf("%d\n",org[ask(rt[l-1],rt[r],1,n,k)]);// 询问对应区间的第k大
}
return 0;
}