引入
考虑$n-1$次多项式$A(x)=a_0+a_1x+…+a_{n-1}x^{n-1}$和$m-1$次多项式$B(x)=b_0+b_1x+…+b_{m-1}x^{m-1}$,可以分别表示为$n$维向量$(a_0,a_1,…,a_{n-1})$和$m$维向量$(b_0,b_1,…,b_{m-1})$
它们相乘获得的多项式$C(x)$的次数显然为$n+m-2$,可以表示为一个$n-m+1$维的向量
朴素的算法如下:
memset(C,0,sizeof(C));
for(int i=0;i<n;++i)
for(int j=0;j<m;++j)
C[i+j]+=A[i]*B[j];
时间复杂度显然是$O(n^2)$,并不那么优秀
多项式的表示
实际上多项式有两种表示方法,系数表达法和点值表达法
系数表达法
一个$n-1$次的多项式的所有系数唯一确定了这个多项式:
\[A(x)=a_0+a_1x+...+a_{n-1}x^{n-1}=\sum_{i=0}^{n-1}a_ix^i\]点值表达法
将一组互不相同的$(x_0,x_1,…,x_{n-1})$代入$A(x)$,得到$n$个取值:$(A(x_0),A(x_1),…,A(x_{n-1}))$,记为:$(y_0,y_1,…,y_{n-1})$
其中$x_i(i\in [0,n-1])$称为插值节点
定理:一个$n-1$次多项式在$n$个不同点的取值唯一确定了该多项式
证明:
假设定理不成立,即存在两个不同的$n-1$次多项式$A(x)$和$B(x)$,使得:$\forall i\in [0,n-1],A(x_i)=B(x_i)$ 那么不妨令$C(x)=A(x)-B(x)$,此时有:$\forall i\in [0,n-1],C(x_i)=0$ 显然$C(x)$是一个$n-1$次多项式,而它却有$n$个互不相同的根,这与代数基本定理矛盾 故原命题成立
如果按照定义求解多项式的点值表示,我们首先需要找到$n$个点,对每个点计算$n$次$a_ix^i$,时间复杂度为$O(n^2)$
多项式乘法
考虑$n-1$次多项式$A(x)$和$m-1$次多项式$B(x)$,他们的乘积$C(x)=A(x)*B(x)$
显然有:$C(x_0)=A(x_0)*B(x_0)$,并且$C(x)$是一个$n-m+2$次多项式
如果我们能找到$n-m+1$个插值节点并且代入计算,我们就能在$O(n+m)$的时间复杂度内获得$C(x)$
如果能快速完成系数表达和点值表达之间的互换,我们就能比$O(n^2)$更快地完成多项式乘法
复数
基本概念
形如$a+bi$这样的数叫做复数,$a$称为实部,$b$称为虚部,$i$称为虚数单位,满足:$i^2=-1$
特别的,当$a=0$时称为虚数,当$b=0$时称为实数
注意:$0$既是实数又是虚数
每一个复数$a+bi$都对应了一个平面向量$(a,b)$,这样的平面被称为复平面
复平面的$x$轴代表实部,称为实轴;$y$轴代表虚部,称为虚轴
复数$z=a+bi$的模长$|z|$定义为$z$在复平面上对应的平面向量的长度,即:$|z|=\sqrt{a^2+b^2}$
所以复数$z$又可以表示为$(\theta,|z|)$,其中$\theta$是实轴的正半轴逆时针旋转到$z$的角度,称为幅角
虚数不能比较大小,两个复数相等当且仅当实部和虚部都相等
运算法则:
- \[(a+bi)+(c+di)=(a+c)+(b+d)i\]
- \[(a+bi)-(c+di)=(a-c)+(b-d)i\]
- \[(a+bi)*(c+di)=ac+bci+bdi+bdi^2=(ac-bd)+(ad+cb)i\]
- \[\frac{a+bi}{c+di}=\frac{(a+bi)*(c-di)}{(c+di)*(c-di)}=\frac{(ac+bd)+(bc-ad)i}{c^2+d^2}\]
复数的加法满足平行四边形法则;乘法满足幅角相加,模长相乘
对于一个复数$z=a+bi$,称$z’=a-bi$为它的共轭复数,有以下两个性质:
- $z*z’=a^2+b^2$
- $\lVert z\rVert=\lVert z’\rVert$
单位根
定义复平面中的单位根$e^{i\theta}=cos\theta+i*sin\theta$
显然单位根的模长为:$sin^2\theta+cos^2\theta=1$
全体单位根构成复平面中的单位圆,如下图所示:
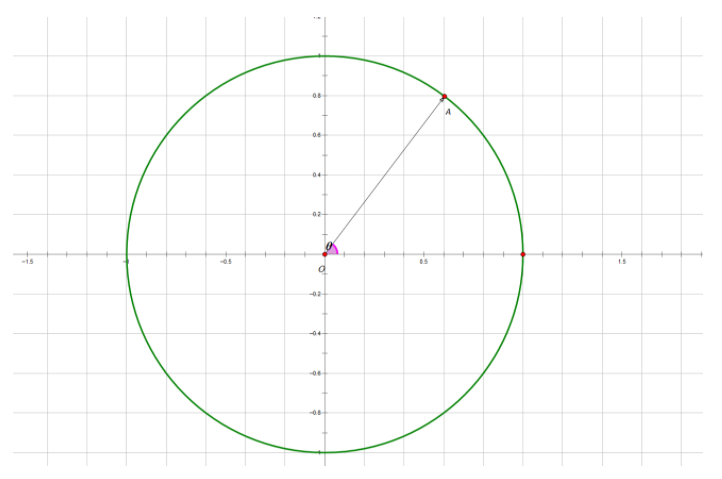
单位根示意图
以单位圆和实轴正半轴的交点作为第一个等分点,把单位圆等分成$n$个部分
以原点为起点,圆的这$n$个等分点作为终点,可以做出$n$个向量
其中幅角为正且幅角最小的向量称为$n$次单位向量,记为:$w_n^1$
上图中$\stackrel{\longrightarrow}{OA}$就是$8$次单位向量,即$w_8^1$
其余的$n-1$个向量记为:$w_n^2,w_n^3,…,w_n^n$,它们之间存在递推关系:$w_n^k=w_n^{k-1}*w_n^1(k\in [2,n])$
不难发现:$w_n^n=w_n^0=1$
实际上:
\[w_n^k=e^{2\pi*\cfrac{k}{n}i}=cos(2\pi*\cfrac{k}{n})+sin(2\pi*\cfrac{k}{n})*i\]单位根有两条重要性质:
折半引理
\[w_{2n}^{2k}=w_n^k\]证明:
\[\begin{aligned} &w_{2n}^{2k} \\ =&cos(2\pi*\cfrac{2k}{2n})+sin(2\pi*\cfrac{2k}{2n})*i \\ =&cos(2\pi*\cfrac{k}{n})+sin(2\pi*\cfrac{k}{n})*i \\ =&w_n^k \end{aligned}\]由此可以引申出:
\[w_{mn}^{mk}=w_n^k\]消去引理
\[w_n^{k+\cfrac{n}{2}}=-w_n^k\]证明:
\[\begin{aligned} &w_n^{k+\cfrac{n}{2}} \\ =&cos(2\pi*\cfrac{k+\cfrac{n}{2}}{n})+sin(2\pi*\cfrac{k+\cfrac{n}{2}}{n})*i \\ =&cos(2\pi*\cfrac{k}{n}+\pi)+sin(2\pi*\cfrac{k}{n}+\pi)*i \\ =&-cos(2\pi*\cfrac{k}{n})-sin(2\pi*\cfrac{k}{n})*i \\ =&-w_n^k \end{aligned}\]离散傅里叶变换
考虑一个$n-1$次的多项式$A(x)=a_0+a_1x+…+a_{n-1}*x^{n-1}$,保证$n=2^x-1,x\in N^+$
此时把$n$次单位根的$0,1,…,n-1$次幂,即:$w_n^0,w_n^1,…,w_n^{n-1}$,代入$A(x)$得到:$A(w_n^0),A(w_n^1),…,A(w_n^{n-1})$
这个过程称为离散傅里叶变换(Discrete Fourier Transform)
朴素$DFT$的复杂度也是$O(n^2)$,必须利用单位根的特殊性质来加速运算
对于:
\[A(x)=a_0+a_1x+a_2x^2+a_3x^3+...+a_{n-2}x^{n-2}+a_{n-1}x^{n-1}\]转化成:
\[A(x)=(a_0+a_2x^2+...+a_{n-2}x^{n-2})+x*(a_1+a_3x^2+...+a_{n-1}x^{n-2})\]令:
\[\begin{aligned} A1(x)=a_0+a_2x+...+a_{n-2}x^{\frac{n-2}{2}} \\ A2(x)=a_1+a_3x+...+a_{n-1}x^{\frac{n-2}{2}} \end{aligned}\]不难发现:
\[A(x)=A1(x^2)+x*A2(x^2)\]下面分两类进行讨论:
- $k\in [0,\cfrac{n-2}{2}],k\in Z$
由折半引理可得:
\[\begin{aligned} &A(w_n^k) \\ =&A1(w_n^{2k})+w_n^k*A2(w_n^{2k}) \\ =&A1(w_{n/2}^k)+w_n^k*A2(w_{n/2}^k) \end{aligned}\]- $k+\cfrac{n}{2}\in [\cfrac{n}{2},n-1],k\in Z$
由折半引理和消去引理可得:
\[\begin{aligned} &A(w_n^{k+n/2}) \\ =&A1(w_n^{2k+n})+w_n^{k+n/2}*A2(w_n^{2k+n}) \\ \because & \ w_n^{2k+n}=w_n^{2k}*w_n^n=w_n^{2k}=w_{n/2}^k \\ \therefore & \ A(w_n^{k+n/2})=A1(w_{n/2}^k)-w_n^k*A2(w_{n/2}^k) \end{aligned}\]注意:上面两类讨论可以保证$k$和$k+\cfrac{n}{2}$取遍了$[0,n-1]$中的$n$个整数,也就保证了可以由这$n$个点值反推出多项式的系数表示,即:该过程是可逆的
同时,如果知道$A1(x)$和$A2(x)$在$w_{n/2}^0,w_{n/2}^1,…,w_{n/2}^{\frac{n-2}{2}}$处的取值,那就能在$O(n)$的时间内求出$A(x)$的取值,而$A1(x)$和$A2(x)$都是$A(x)$一半的规模,可以转化为子问题递归求解,其时间复杂度类似于归并排序:$O(nlogn)$
离散傅里叶反变换
将点值表示的多项式转化为系数表示的过程叫做离散傅里叶反变换(Inverse Discrete Fourier Transform),上面提到过$DFT$是可逆的,$IDFT$就是它的逆过程
假设:$(d_0=A(w_n^0),d_1=A(w_n^1),…,d_{n-1}=A(w_n^{n-1}))$为$(a_0,a_1,..,a_{n-1})$经过$DFT$得到的结果
构造一个多项式:$F(x)=d_0+d_1x+…+d_{n-1}x^{n-1}$
设向量$(c_0,c_1,…,c_{n-1})$中的$c_k$是$F(x)$在$x=w_n^{-k}$处的点值表示,即:
\[c_k=F(w_n^{-k})=\sum_{i=0}^{n-1}d_i*(w_n^{-k})^i\]考虑把$d_i=A(w_n^i)$代入上式:
\[\begin{aligned} &c_k \\ =&\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j*(w_n^i)^j)*(w_n^{-k})^i \\ =&\sum_{j=0}^{n-1}a_j*\sum_{i=0}^{n-1}(w_n^i)^j*(w_n^{-k})^i \\ =&\sum_{j=0}^{n-1}a_j*\sum_{i=0}^{n-1}(w_n^i)^{j-k} \end{aligned}\]令:
\[S(j,k)=\sum_{i=0}^{n-1}(w_n^i)^{j-k}\]再令:
\[\delta=j-k\]则:
\[s(j,k)=w_n^0+w_n^\delta+...+w_n^{(n-1)\delta}\]不难看出$S(j,k)$实际上是一个等比数列的前$n$项和,公比为$w_n^\delta$,首项为$w_n^0=1$
下面分两类进行讨论:
- $j-k=0$
此时显然有:$\delta=0,w_n^\delta=1$
得出:$S(j,k)=n$
- $j-k \not = 0$
代入等比数列求和公式:
\[S(j,k)=\cfrac{w_n^0*[(w_n^\delta)^n-1]}{w_n^\delta-1}=\cfrac{(w_n^n)^\delta-1}{w_n^\delta-1}=\cfrac{1-1}{w_n^\delta-1}=0\]所以得出结论:
\[S(j,k)=[j==k]*n\]把上述结论代回$c_k$的表达式:
\[\begin{aligned} &c_k \\ =&\sum_{j=0}^{n-1}a_j*S(j,k) \\ =&\sum_{j=0}^{n-1}a_j*[j==k]*n \\ =&a_k*n \end{aligned}\]再捋一捋他们的关系:
\[a_k\stackrel{w_n^k}{\longrightarrow}d_k\stackrel{w_n^{-k}}{\longrightarrow}c_k\]上式中每一个箭头就代表了一次$DFT$
实际上,对$DFT$得到的结果换一种插值再做一次$DFT$,就能起到$IDFT$的作用,因为$a_k$和$c_k$之间有着密切的联系
注意:$w_n^{-k}$是$w_n^k$的共轭复数
在C中的实现
首先来看看$fft$向下递归时下标的变化情况:
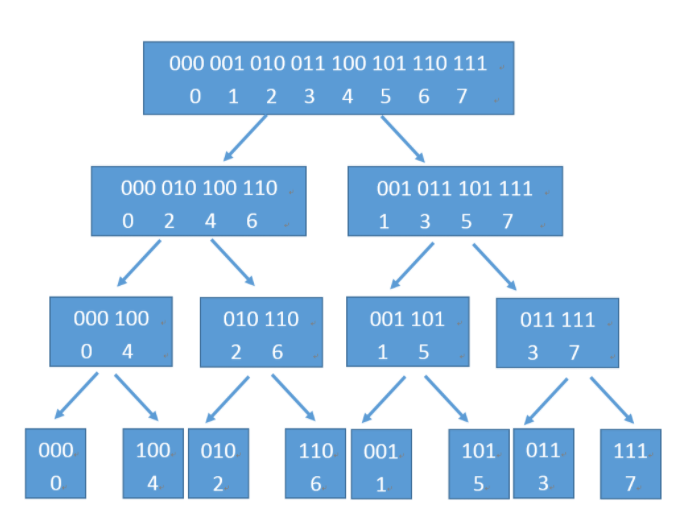
下标变化
所以可以先将原数组调整成最底层的位置,然后从倒数第二层由底向上迭代计算,这种算法被称为实现$fft$的$Cooley-Tukey$算法
最底层位置的数字遵循规律:翻转了原顺序每个数字的二进制表示
如下所示:
| 原顺序 | 原顺序二进制 | 最底层顺序 | 最底层顺序二进制 |
|---|---|---|---|
| 0 | (000) | 0 | (000) |
| 1 | (001) | 4 | (100) |
| 2 | (010) | 2 | (010) |
| 3 | (011) | 6 | (110) |
| 4 | (100) | 1 | (001) |
| 5 | (101) | 5 | (101) |
| 6 | (110) | 3 | (011) |
| 7 | (111) | 7 | (111) |
观察最底层顺序,实际上也是从$0$开始,用一种特殊的顺序得到的:最高位加$1$,向低位进位
用代码写出来就是把高位所有连续的的$1$置为$0$,并且把第一个$0$置为$1$:
void getOrd(int n) {
int i=0,j=0;
for(;i<n;++i) {
ord[i]=j;
int mask=n/2;// highest position
while(j&mask) j&=~mask,mask/=2;// change all 1 to 1
j|=mask;// change 0 to 1
}
}
现在考虑如何合并左右两部分答案:
假设当前层有$n$项需要处理,并且此时$A1(w_{n/2}^k)$和$A2(w_{n/2}^k)$分别存放在$a[k]$和$a[k+n/2]$当中
引入一个$buf$数组,我们希望把$A(w_n^k)$和$A(w_n^{k+n/2})$的结果分别存放在$buf[k]$和$buf[k+n/2]$当中
合并的操作可以表示为:
buf[ k ] = a[ k ] + omega(n, k) * a[ k + n / 2 ];
buf[ k + n / 2 ] = a[ k ] - omega(n, k) * a[ k + n / 2 ];
不妨改变合并顺序,引入一个变量来实现原地更新:
tmp = omega(n, k) * a[ k + n / 2 ];
a[ k + n / 2 ] = a[k] - tmp;
a[ k ] += tmp;
最后总的代码如下:
#include <stdio.h>
#include <math.h>
#define PI acos(-1)
#define MAXN 5000005
/*
Definition of Complex Number
*/
typedef struct{
double r,i;
}Complex;
void setR(Complex *c,double r){c->r=r;}
void setI(Complex *c,double i){c->i=i;}
Complex initComplex(double r,double i){Complex c;setR(&c,r);setI(&c,i);return c;}
double getR(Complex c){return c.r;}
double getI(Complex c){return c.i;}
Complex add(Complex a,Complex b){return initComplex(a.r+b.r,a.i+b.i);}
Complex sub(Complex a,Complex b){return initComplex(a.r-b.r,a.i-b.i);}
Complex mul(Complex a,Complex b){return initComplex(a.r*b.r-a.i*b.i,a.r*b.i+a.i*b.r);}
Complex div(Complex a,double b){return initComplex(a.r/b,a.i/b);}
Complex coj(Complex a){return initComplex(a.r,-a.i);}
void swap(Complex *a,Complex *b){Complex c=*a;*a=*b;*b=c;}
/*
Rader Sort
*/
int ord[MAXN];
void getOrd(int n) {
int i=0,j=0;
for(;i<n;++i) {
ord[i]=j;
int mask=n/2;// highest position
while(j&mask) j&=~mask,mask/=2;// change all 1 to 1
j|=mask;// change 0 to 1
}
}
/*
Cooley-Tukey
*/
void trans(Complex a[],int n,int flg) {// 1 for dft,-1 for idft
// change the order
int i=0;
for(;i<n;++i)
if(i<ord[i])
swap(a+i,a+ord[i]);
// from low to high
int mid=1,L=0;
for(;mid<n;mid*=2) {
Complex ww=initComplex(cos(PI/mid),flg*sin(PI/mid)),tmp;
for(L=0;L<n;L+=mid*2) {
Complex w=initComplex(1.0,0.0);
for(i=L;i<L+mid;++i,w=mul(w,ww))
tmp=mul(w,a[i+mid]),
a[i+mid]=sub(a[i],tmp),
a[i]=add(a[i],tmp);
}
}
}
/*
fft
*/
void dft(Complex a[],int n){trans(a,n,1);}
void idft(Complex a[],int n) {
trans(a,n,-1);
int i=0;
for(;i<n;++i) a[i]=div(a[i],n);
}
实际操作中有两点需要特别注意:
精度调整
$double$强制转换成$int$会丢精度,最好加上$0.5$之后再转换
长度调整
上述$fft$模板仅用于数组长度为$2^x$的情况,具体情况具体调整
C的swap函数
之前想用$C$写$swap$函数,大概像下面这样:
void swap1(int *a,int *b) {
int *c=a;
a=b;
b=c;
}
经过测试,完全不能交换$a$和$b$中储存的数字,必须写成下面这样:
void swap2(int *a,int *b) {
int c=*a;
*a=*b;
*b=c;
}
单纯交换指针是不行的,应该交换指针指向的数字
测试代码如下:
#include <stdio.h>
void swap1(int *a,int *b) {
int *c=a;
a=b;
b=c;
}
void swap2(int *a,int *b) {
int c=*a;
*a=*b;
*b=c;
}
int main() {
int a=1,b=2;
printf("%d %d\n",a,b);
swap1(&a,&b);
printf("%d %d\n",a,b);
swap2(&a,&b);
printf("%d %d\n",a,b);
}