对于串“ABBA”,建立出来的回文自动机如下图:
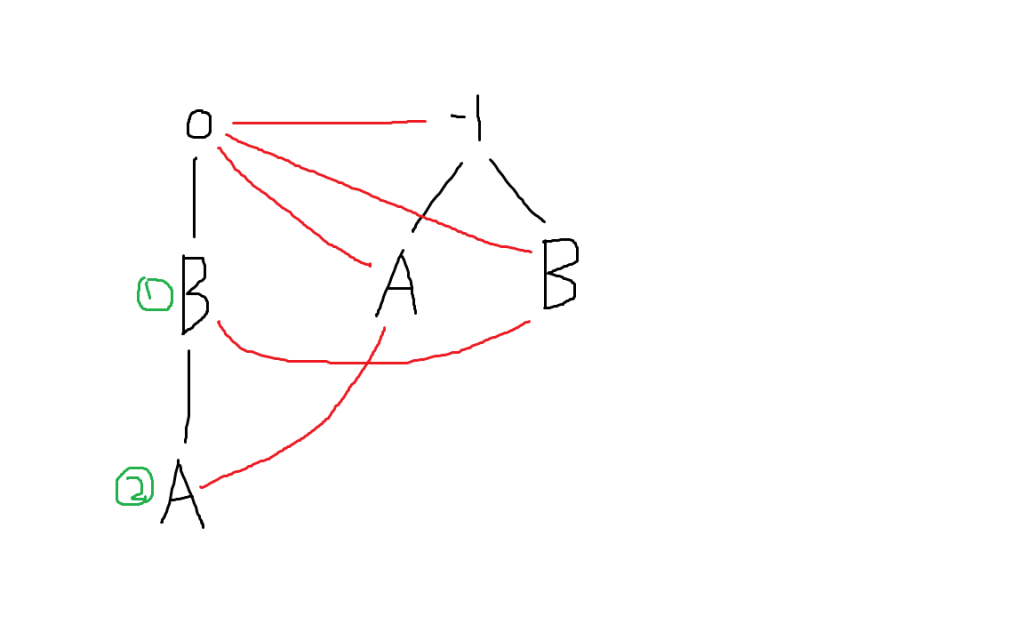
回文自动机
有一些说明:
- 上图中黑线表示后缀边,红线表示$fail$边
- 每个节点都代表了一个回文子串,例如图中①号节点代表了$BB$,②号节点代表了$ABBA$
- 一个回文自动机实际上包含两棵树,分别代表奇偶回文子串
- 每条后缀边上都有一个字符,若某点对应的回文子串为$S$,后缀边上的字符为$c$,那么这条后缀边指向了代表$c+S+c$这个回文串的节点
- 把奇数回文子串的初始长度设为$-1$就是为了满足后缀边的特性
模板如下:
/*
fail[x]:x节点失配之后跳转到不等于自身的最长后缀回文子串
len[x]:以x结尾的最长回文子串长度
num[x]: 与”以x结尾的最长回文子串“本质不同的子串个数
cnt[x]:与”以x结尾的最长回文子串“本质相同的子串个数
(注意上面两个数组完全相反)
son[x][c]:编号为x的节点表示的回文子串在两边添加字符c之后变成的回文子串编号
s[x]:第x次添加的字符,s数组即原字符串
tot:总节点个数,节点编号由0到tot-1
last:最后一个新建立节点的编号
cur:当前节点在PAM上的父亲编号
*/
struct PAM
{
int tot,last,n,cur;
int fail[N],len[N],same[N],diff[N],son[N][26];
char s[N];
int get(int p,int x)
{
while(s[x-len[p]-1]!=s[x])
p=fail[p];
return p;
}
int newnode(int x)
{
len[tot]=x;
return tot++;
}
void build()
{
scanf("%s",s+1);
s[0]=-1,fail[0]=1,last=0;
newnode(0),newnode(-1);
for(n=1;s[n];++n)
{
s[n]-='a';
cur=get(last,n);
if(!son[cur][s[n]])
{
int now=newnode(len[cur]+2);
fail[now]=son[get(fail[cur],n)][s[n]];
diff[now]=diff[fail[diff[now]]]+1;
son[cur][s[n]]=now;
}
same[last=son[cur][s[n]]]++;
}
for(int i=tot-1;i>=0;--i)
same[fail[i]]+=same[i];
}
}pam;