用来解线性方程组的算法。
每次选取一列,即对应的一个未知变量,把关于这个未知变量最大的系数放到第一行去,以达到消元时减小精度误差的目的,之后回代求解。
复杂度$O(n^3)$。
基本步骤如下:
首先我们找到当前列中最大系数的位置,假设为$mx$,并且交换$mx$与$a[i][i]$。
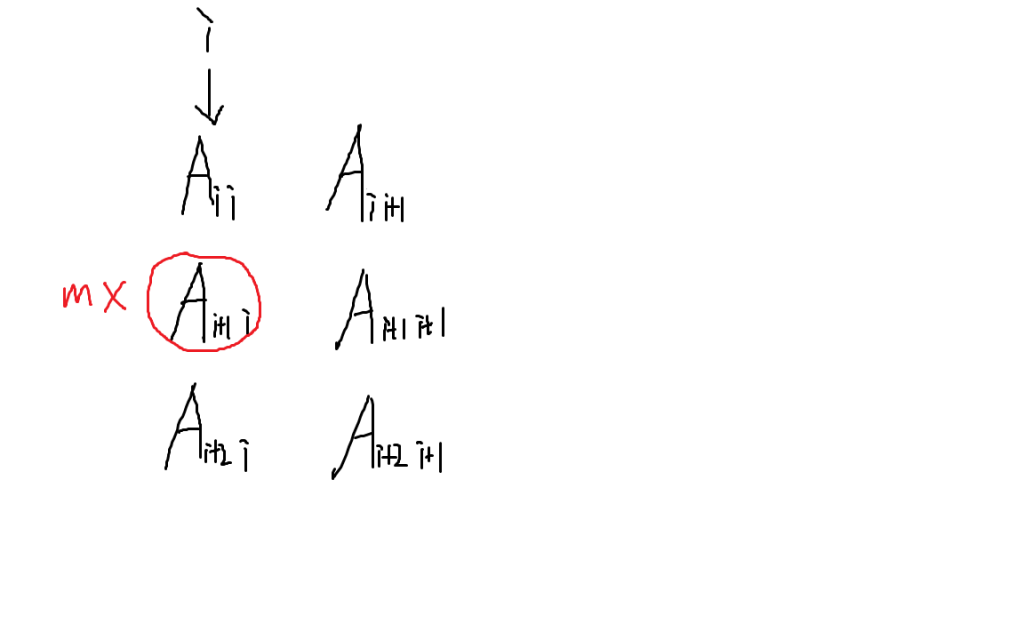
第一步
随后对每个含有$i$对应的未知元的方程使用加减消元公式:
\[a[j][k]-=a[i][k]*a[j][i]/a[i][i]\]就像用下图中的下一行减去上一行:
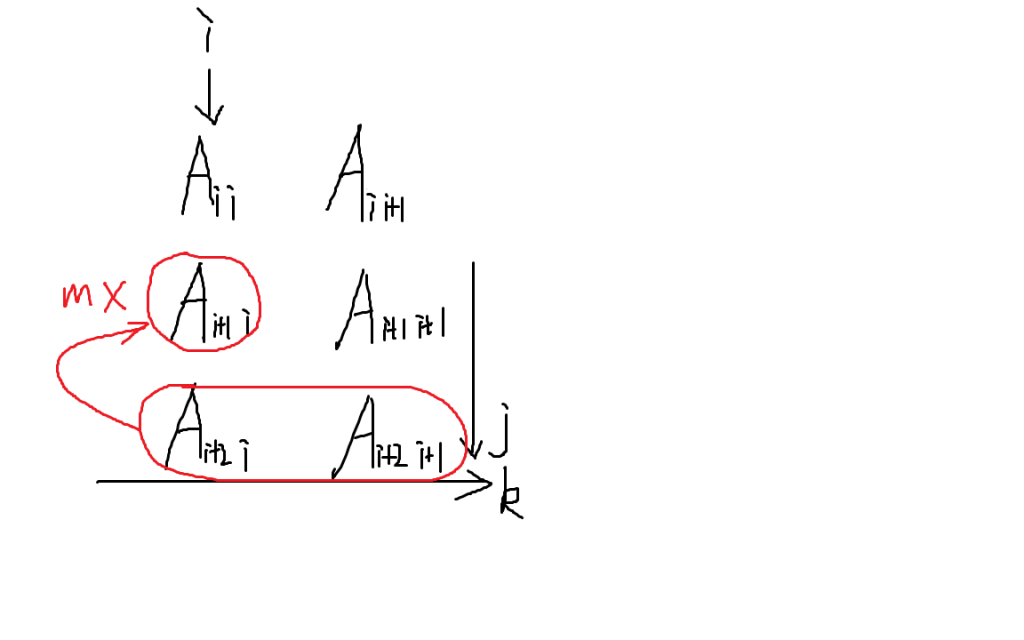
第二步
模板如下:
/*
a数组是由n*n的系数矩阵和一列常数构成,第n+1列是常数
No Solution表示方程组没有唯一解
gauss消元是会丢精度的,要注意调整eps的取值
*/
void gauss(db a[10005][10005]) {
for(int i=1;i<=n;++i) {
int mx=i;
for(int j=i+1;j<=n;++j)
if(fabs(a[j][i])>fabs(a[mx][i]))
mx=j;
if(fabs(a[i][i])<eps) {//the maxium value is 0.0
puts("No Solution");
return;
}
if(mx!=i) {
for(int j=1;j<=n+1;++j)
swap(a[i][j],a[mx][j]);
}
for(int j=1;j<=n;++j) {
if(j!=i) {
db tmp=a[j][i]/a[i][i];
for(int k=i+1;k<=n+1;++k)
a[j][k]-=a[i][k]*tmp;
}
}
}
for(int i=1;i<=n;++i)
printf("%.2lf\n",a[i][n+1]/a[i][i]);
}
关于解的存在性的结论如下:
- 若存在系数全0常数不为0的行,无解
- 若系数不全为0的行恰好有n个,有唯一解
- 若系数不全为0的行数k小于n,则说明一共有k个主元,n-k个自由元,有无穷多解
高斯消元还有一种特别的版本——异或方程组,题目见P2962 [USACO09NOV]灯Lights。
题解地址:题解。
模板如下:
/*
gauss函数返回的是方程组是否有自由元
异或方程组有2^(自由元个数)个解
*/
bool gauss(int a[maxn][maxn]) {
bool no=1;
for(int i=1;i<=n;++i) {
int mx=i;
while(mx<=n&&!a[mx][i]) ++mx;
if(mx>n) {
no=0;
continue;
}
swap(a[i],a[mx]);
for(int j=1;j<=n;++j) {
if(i==j||!a[j][i]) continue;
for(int k=i+1;k<=n+1;++k)
a[j][k]^=a[i][k];
a[j][i]=0;
}
}
return no;
}