考虑这样一个问题:
给定一棵有n个点的树,询问树上距离为k的点对是否存在。
朴素的想法是用$O(n^2)$时间枚举点对,然后在$O(log(n))$时间内利用$LCA$找到两点间距离,看是否为$k$即可,但是在$n$较大的情况下必然不可行。
考虑树上的所有路径本质上只有两类,如下图:
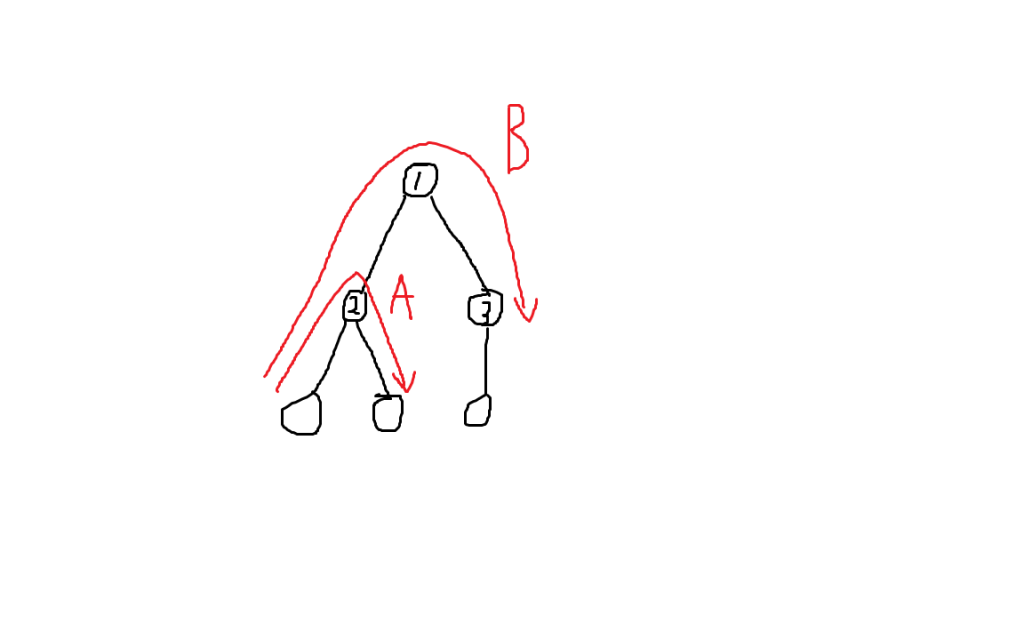
树上路径
假设目前以①号节点为根,那么$A$类路径代表①号节点某个子树中的路径,$B$类路径则代表经过①号节点的路径。
可以发现如果能在$O(n)$时间内解决$B$类路径的计数问题,那么就可以利用分治的思想,控制遍历层数在$O(log(n))$,递归地对每个①号节点的子树求解$B$类路径。
这样就把所有的路径归一成了不同子树上$B$类路径的求解,这也是点分治的基础。
点分治首先考虑不同子树对当前根的影响,然后递归计算下去,基本步骤如下:
- 找到树的重心,维持树深在$O(log(n))$附近
- 求出每个点到当前根的距离以及这个点属于哪颗子树
- 执行$cal$函数,计算答案贡献
- 删除当前节点,对子树进行递归
不同的题目的cal函数大相径庭,下面贴上 P3806 【模板】点分治1 的代码:
/*
getrt:获取树的重心
getdis:获取距离
cal:计算答案贡献
div:分治函数
*/
#include <bits/stdc++.h>
using namespace std;
const int maxn=500005;
const int inf=0x3f3f3f3f;
int n,m,a,b,c,ask[maxn];
bool have[maxn*20],can[maxn],vis[maxn];
vector<int> g[maxn],v[maxn];
int sum,sz[maxn],son[maxn],rt;
int rem[maxn],dis[maxn];
queue<int> q;
void getrt(int x,int f){
sz[x]=1,son[x]=0;
for(int i=0;i<g[x].size();++i){
int y=g[x][i];
if(vis[y]||y==f) continue;
getrt(y,x);
sz[x]+=sz[y];
son[x]=max(son[x],sz[y]);
}
son[x]=max(son[x],sum-sz[x]);
if(son[x]<son[rt]) rt=x;
}
void getdis(int x,int f){
rem[++rem[0]]=dis[x];
for(int i=0;i<g[x].size();++i){
int y=g[x][i];
if(vis[y]||y==f) continue;
dis[y]=dis[x]+v[x][i];
getdis(y,x);
}
}
void cal(int x){
dis[x]=0;
for(int i=0;i<g[x].size();++i){
int y=g[x][i];
if(vis[y]) continue;
rem[0]=0;//clear the rem every time
dis[y]=v[x][i];
getdis(y,x);
for(int i=rem[0];i;--i){
for(int j=1;j<=m;++j){
if(can[j]) continue;
if(ask[j]>=rem[i])
can[j]|=have[ask[j]-rem[i]];
}
}
for(int i=rem[0];i;--i){
have[rem[i]]=1;
q.push(rem[i]);
}
}
while(!q.empty()){
int f=q.front();
have[f]=0;
q.pop();
}
}
void div(int x){
vis[x]=1,have[0]=1;
cal(x);
for(int i=0;i<g[x].size();++i){
int y=g[x][i];
if(vis[y]) continue;
sum=sz[y];
rt=0;
son[rt]=inf;
getrt(y,0);
div(rt);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n-1;++i){
scanf("%d%d%d",&a,&b,&c);
g[a].push_back(b);
g[b].push_back(a);
v[a].push_back(c);
v[b].push_back(c);
}
for(int i=1;i<=m;++i) scanf("%d",&ask[i]);
sum=n;
rt=0;
son[rt]=inf;
getrt(1,0);
div(rt);
for(int i=1;i<=m;++i){
if(can[i]) puts("AYE");
else puts("NAY");
}
return 0;
}
点分治的清空操作真的是很恶心,一定要记得清空$bool$数组以及更改当前子树中点的数量。