建立在trie树上的kmp,可以进行多模式串的匹配。
即对于一个文本串,返回它与哪些模式串匹配的最后位置的下标,详细参见代码注释。
代码
#define fo(i,a,b) for(int i=a;i<b;++i)
int n,ans[maxn],l2[maxn],same[maxn];
char s[maxn],t[maxn];
queue<int> q;
struct AC_AUTO{
int c[maxn][26],val[maxn],fail[maxn],cnt;
int vis[maxn];
void ins(char *s,int pos) {
int len=strlen(s),now=0;
fo(i,0,len) {
int v=s[i]-'a';
if(!c[now][v]) c[now][v]=++cnt;
now=c[now][v];
}
if(val[now]) same[pos]=val[now];//same数组用于去重,解决重复模式串的问题
else val[now]=pos;
}
void build() {
fo(i,0,26)
if(c[0][i])
fail[c[0][i]]=0,
q.push(c[0][i]);
while(!q.empty()) {
int u=q.front();
q.pop();
fo(i,0,26) {
if(c[u][i])
fail[c[u][i]]=c[fail[u]][i],
q.push(c[u][i]);
else
c[u][i]=c[fail[u]][i];
}
}
}
void query(char *s) {
int len=strlen(s),now=0;
fo(i,0,len) {
now=c[now][s[i]-'a'];
for(int t=now;t;t=fail[t]) {
if(val[t]&&!vis[now])
//这里实际上说明下标为val[t]的串在i位置被匹配到了,注意i是匹配结束的位置
ans[val[t]]=mmax(ans[val[t]],len-i-1,i-l2[val[t]]+1);
//l2是原模式串的长度,用于更新答案。
}
vis[now]=1;
//这里我的理解有误,如果要求某个模式串只能出现一次,这里的vis就必须设置为1,或者也可以把val[t]更改成0
}
}
}ac;
关于AC自动机的某些有用的性质总结如下:
性质1
fail指针指向与该节点表示串后缀相等的且长度最大的串(或前缀)的节点
读起来有点拗口,实际上挺好理解,比如下面这张图:
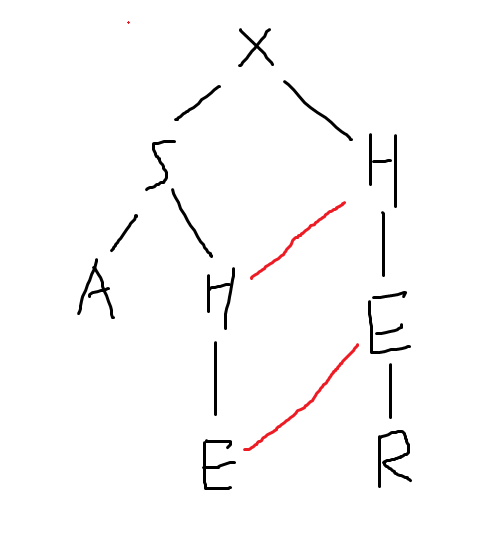
fail边示意图1
除了两条红边之外其他所有节点的$fail$边都指向根节点$X$。
性质2
通俗来说:
fail边是与当前后缀位置最长匹配的前缀位置
如下图:
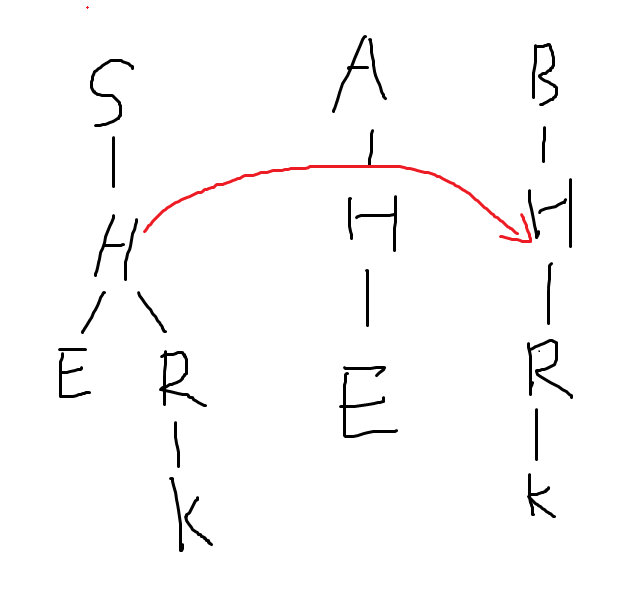
fail边示意图2
性质3
有一个问题:如果我建立了一个AC自动机并且把它的fail指针倒序建立成了一棵树,这棵树又有什么性质呢?
对于fail边示意图1建出来的这样的树如下,我们把它称为fail树。
实际上可以理解为每个节点都是一个字符串(类似于回文自动机):
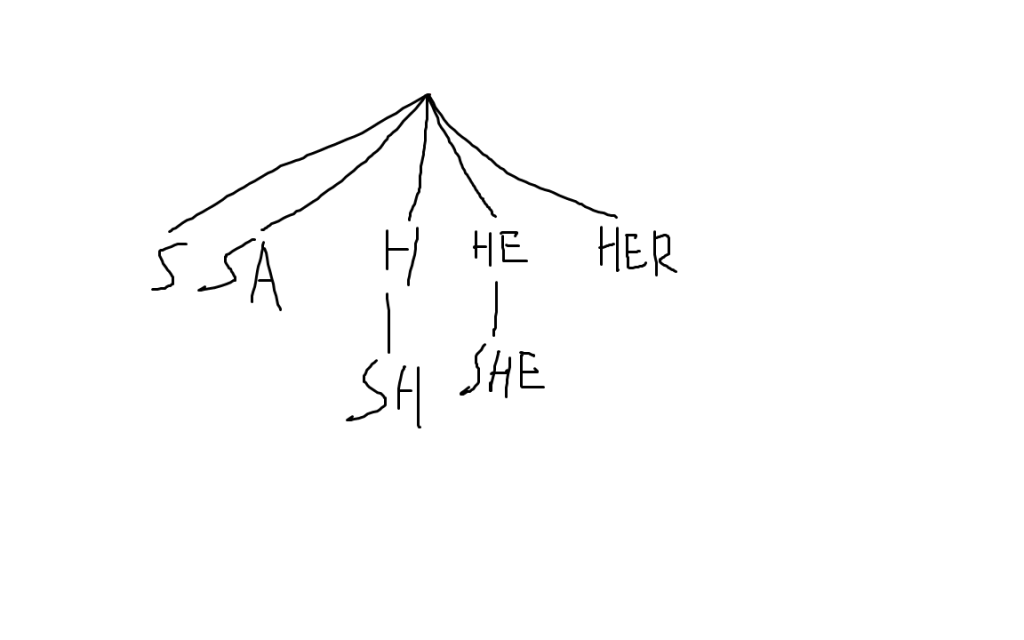
fail树
考虑这样一个问题:$a$、$b$两串同时处于AC自动机当中,那么$a$串在$b$串中出现了多少次呢?
结论如下:
每个节点保存一下它属于多少字符串,作为该节点的权值。
然后某个节点表示的字符串在整个字典中出现的次数相当于其在Fail树中的子树的权值的和。
上图当中,$H$出现了两次,并且$HE$也出现了两次。